What is Gradient Descent?
Gradient Descent is a fundamental optimization algorithm used in machine learning and deep learning to minimize a function. It aims to find the minimum value of a function by iteratively moving in the direction of the steepest descent, as defined by the negative of the gradient.
In machine learning, this function typically represents the loss or error of a model, and minimizing it leads to a more accurate model. The algorithm updates the parameters of the model, such as weights in neural networks, by taking steps proportional to the negative of the gradient of the function at the current point.
What is stochastic gradient descent?
Stochastic Gradient Descent (SGD) is a variant of the gradient descent algorithm. It differs by updating the model's parameters using only a single or a few training examples at a time. This approach can lead to faster convergence since it updates the model more frequently. However, the path to convergence can be noisier or more erratic compared to standard gradient descent, which uses the entire dataset to compute the gradient at each step.
What is gradient descent in machine learning?
In machine learning, gradient descent is used to optimize the parameters of models like neural networks, linear regression, and logistic regression. It does so by minimizing a cost function, which measures the difference between the model's predictions and the actual data. By iteratively adjusting the parameters in the direction that reduces the cost, gradient descent seeks to improve the model's predictions.
What is the stochastic gradient descent package in R? and Can stochastic gradient descent be used with linear regression?
In R, packages like sgd, keras, and tensorflow provide functionalities for implementing stochastic gradient descent. SGD can indeed be used with linear regression; it's particularly useful for large datasets where using standard gradient descent might be computationally expensive. SGD offers a faster but less precise alternative, iterating over smaller subsets of data to converge to an optimal solution.
What is the Gradient Descent Algorithm in Machine Learning?
The Gradient Descent Algorithm in machine learning is an iterative optimization algorithm used to minimize the cost function in various machine learning models. It involves calculating the gradient (or derivative) of the cost function with respect to the model parameters, and then adjusting those parameters in the opposite direction of the gradient. By repeatedly performing these steps, the algorithm seeks to find the parameter values that minimize the cost function, leading to an optimized model.
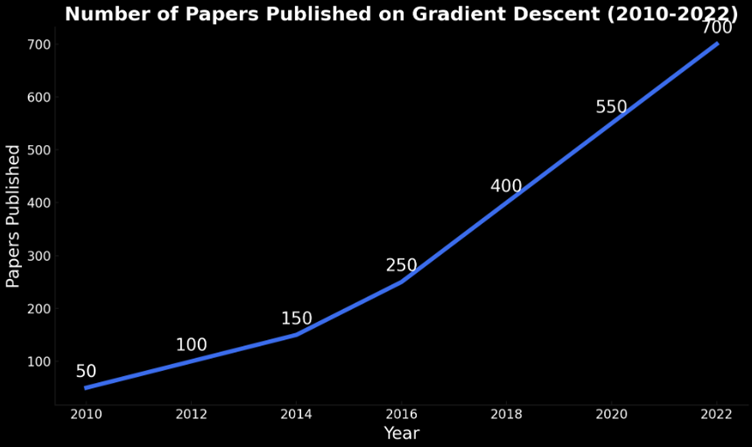
Interesting Data about Gradient Descent
Here are some fascinating statistics and insights about Gradient Descent:
Trends in Algorithm Usage: Over the years, the use of Gradient Descent and its variants (like Stochastic Gradient Descent) in machine learning has seen significant growth, especially with the rise of deep learning.
Efficiency in Training Large Models: Studies have shown that Stochastic Gradient Descent can be significantly faster than traditional Gradient Descent when training large-scale models, such as those in deep learning.
Popularity in Academia and Industry: Gradient Descent remains a popular topic in academic research, with numerous papers published annually, and is widely used in industry for training various machine learning models.